Trasmissione luminosa
La radiazione elettromagnetica
Un corpo a temperatura superiore allo zero assoluto emette radiazioni elettromaghetiche in tutte le direzioni. La potenza radiante (W) è in genere rapportata alla superficie che la emette, per cui si valuta, della radiazione, la potenza specifica (W/m2). La radiazione complessiva comprende un ampio campo di lunghezze d'onda, ciascuna dotata di una propria energia. Si definisce un corpo ideale detto corpo nero, assunto come riferimento per tutti gli altri corpi, quello che emette la massima energia per ogni lunghezza d'onda e per ogni temperatura. Il corpo nero, oltre che perfetto emettitore è anche un perfetto assorbitore, cioè assorbe tutta l'energia radiante che riceve senza alcuna riflessione. Per questo motivo è detto nero in quanto il colore percepito è dato dalla composizione spettrale della luce riflessa. Se un corpo riflette tutta la luce ricevuta appare bianco, se l'assorbe, nero. In pratica può essere realizzato praticando un piccolo foro su di in corpo cavo. Il foro si comporta come il corpo nero. La luce è una porzione dell'intero spettro elettromagnetico compresa tra le lunghezze d'onda di 400 ed i 760 nm. L'energia totale emessa dal corpo nero è regolata dalla legge di Stefan-Boltzmann: il potere emissivo del corpo nero, espresso inW/m2, è dato da
En = sn*T4
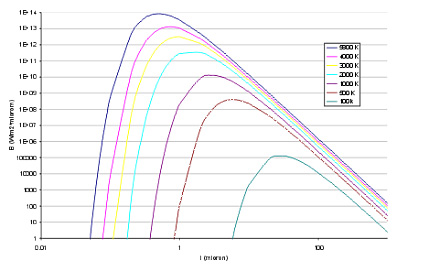
sn= 5.67*10-8 (W/m2*K4) Costante di Stefan-Boltzmann T: temperatura assoluta del corpo (K) En è il potere emissivo totale ed è la somma della radiazione emessa in tutte le lunghezze d'onda. Si definisce potere emissivo monocromatico (o spettrale) la potenza specifica emessa dal corpo alla temperatura T, ad una data lunghezza d'onda e per unità di lunghezza d'onda. Cioè la potenza specifica di quella lunghezza d'onda diviso la lunghezza d'onda stessa. Quindi è misurata in (W/m3 : più comunemente W/m2*micron). Vale per il corpo nero la legge di distribuzione di Planck, illustrata in figura fs.1
Enl=C1/(l5(eC2/lT - 1))
- C1=2phc ; C2=hc/k
- h: costante di Planck
- c: velocit` della luce
- k: costante di Boltzmann
Trasmissione luminosa: te
La trasmissione luminosa riguarda il comportamento di una vetrata rispetto alla luce (cioè, come detto, le radiazioni elettromagnetiche comprese tra 0.4 ed i 0.76 mm). L'andamento dell'energia emessa da una sorgente all'interno di quell'intervallo è dipendente dalla natura della sorgente e dalla sua temperatura. Nello studio delle proprietà ottiche e colorimetriche si usano gli illuminanti standard. Per determinare la trasmissione luminosa si usa il D65, la cui emissione spettrale è mostrata dalla curva di figura.
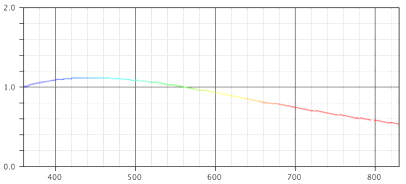
fs.2 Diagramma realizzato con l' applicazione della pagina CIE Spectral Display di Bruce Lindbloomz
Poichè l'occhio non è ugualmente sensibile a tutte le lunghezze d'onda dello spettro elettromagnetico visibile, i valori dell'illuminante per una data lunghezza d'onda sono moltiplicati per il fattore di visibilità relativi a quella lunghezza d'onda. Si ottiene, per l'illuminante D65 , la curva di figura fs.3
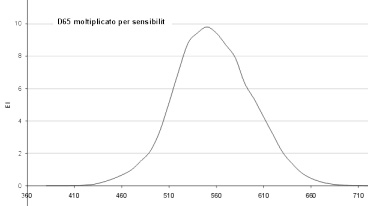
L'area delimitata dalla curva rappresenta la totale energia visibile, cioè il flusso luminoso emesso, nel caso specifico dall'illuminante D65. Il calcolo della trasmissione luminosa consiste nel tracciare la curva spettrale dell'energia visibile trasmessa pesata secondo la sensibilità spettrale dell'occhio e fare il rapporto tra l'area che delimitata da questa curva e l'area della curva dell'illuminante. La figura illustra il confronto. Nelle figura fs.3 ed fs.4, i valori della curva D65 sono stati predeterminati in modo che l'area valga 100. Nella figura fs.4 è tracciato il grafico della luce trasmessa da un vetro chiaro. Si ha, in tal caso, una trasmissione luminosa elevata, attorno al 90%.
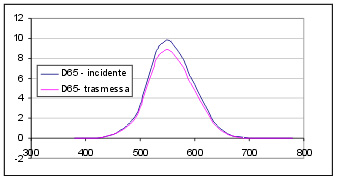
La trasmissione luminosa rappresenta dunque il rapporto tra il flusso luminoso trasmesso ed il flusso luminoso incidente. Per tracciare la curva dell'energia visibile trasmessa occorre disporre della curva di trasmittanza spettrale tl determinata con misure di laboratorio. Esempi di queste curve sono mostrati, per diversi tipi di vetro, nelle figure fs.6,7,8,9.
- Vetro Float chiaro da 6 mm
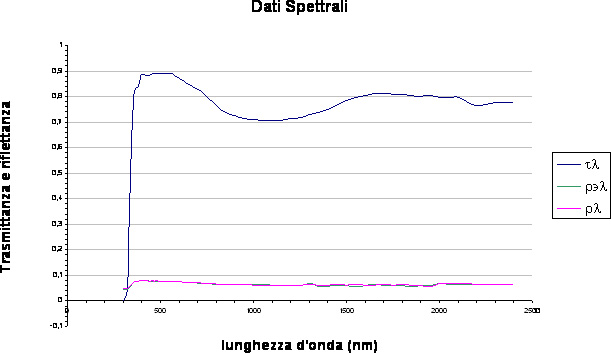
- Vetro bassoemissivo magnetronico da 4 mm
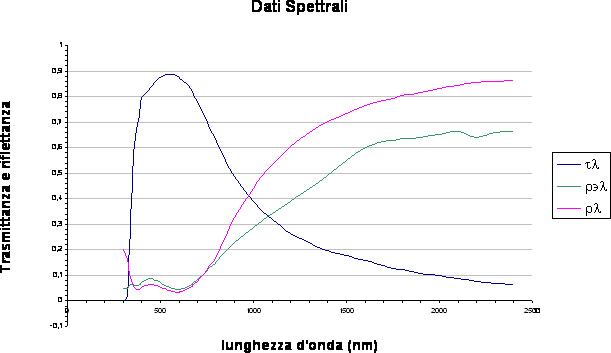
-Vetro bassoemissivo pirolitico da 6 mm
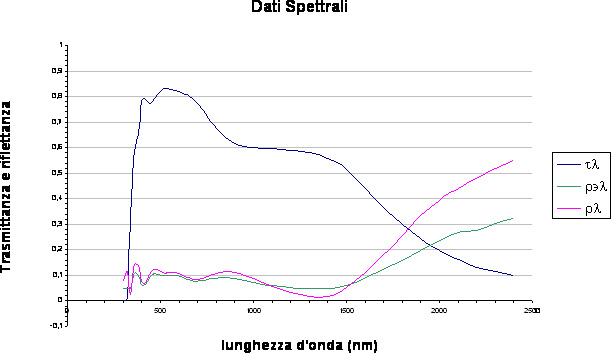
- Vetro a controllo solare da 6 mm
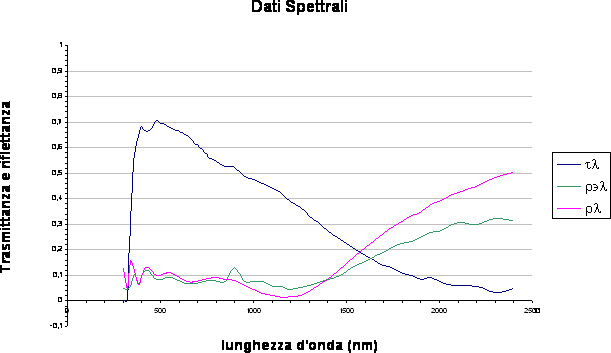
Nelle figure precedenti, oltre alla trasmittanza spettrale compaiono altre curve, le riflettanze spettrali ( r l r'l ) dei delle due facce del vetro, necessarie per poter determinare con il calcolo, condotto in base alla norma EN 410, la trasmissione e, come vedremo, il fattore solare, di vetri composti (doppi vetri e tripli vetri). Per le diverse composizioni vetrarie bisogna dunque disporre dei dati spettrali dei vetri componenti. Essi sono: Per un vetro chiaro
- Trasmittanza spettrale (tl)
- Riflettanza spettrale (rl)
Per un vetro bassoemissivo
- Trasmittanza spettrale (tl)
- Riflettanza spettrale (rl) lato trattato
- Riflettanza spettrale (rl) lato non trattato
- Emissività normale lato trattato
Quando si realizza un doppio vetro infatti, per il calcolo dell'energia trasmmessa occorre considerare il gioco delle riflessioni interne all'intercapedine. La trasmittanza spettrale risultante non è infatti semplicemente il prodotto delle due trasmittanze, come si potrebbe pensare (senza riflettere è proprio il caso di dire) ma da questa espressione t = t1*t2/(1 - r1b*r2) dove t1e t2 sono le trasmittanze spettrali dei due vetri componenti, e r1b e r2 le riflettanze spettrali sul lato opposto a quello incidente del vetro esterno e della parte incidente del vetro interno.

